CS 180 Project 2

Vivian Liu

Website URL: https://vzliu.github.io/cs180/websites/proj2.html

Website template credit to CS 184

Overview

In this project I applied a variety of filters to sharpen and blur images, create hybrid images, and did multiresolution blending.


Part 1: Fun with Filters

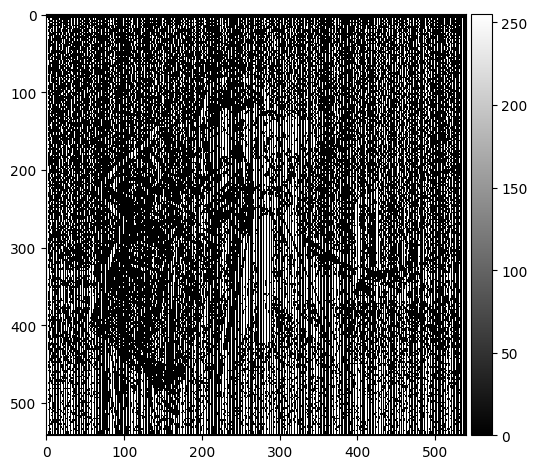
Part 1.1: Finite Difference Operator

In this part, I took the partial derivative in x and y of the cameraman image by convolving with finite difference operators D_x and D_y. I then calculated the gradient magnitude and binarized to get edges. To compute the gradient magnitude, which measures the rate of change in pixel intensity, I used partial derivatives of the image intensity function in both the horizontal and vertical directions. Then, I combined these two changes to get the "gradient magnitude." The bigger the gradient magnitude, the more likely there is an edge due to drastic changes in that area in an image.

Original
Convolve with D_x (Horizontal)
Convolve with D_y (Vertical)
Gradient Magnitude


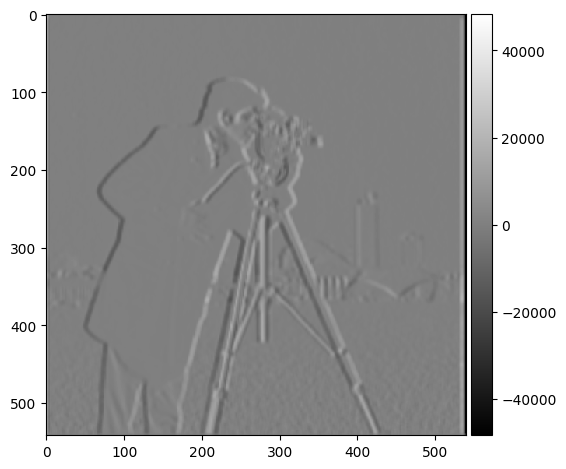
Part 1.2: Derivative of Gaussian (DoG) Filter

As seen above, the finite difference filter produced images that were still rather noisy, especially in the background. To address this, I convolve with a Gaussian filter to blur images, which helped to reduce noise in the background of images, then convolve again with the finite difference operators.

Blurred Cameraman
2 Convolutions dx
2 Convolutions dy
2 Convolutions Gradient Magnitude

What differences do you see?
I see that the background noise has been significantly reduced. The edges of the man and camera are also more pronounced.

Blurred Cameraman
1 Convolution dx
1 Convolution dy
1 Convolution (Derivative of Gaussian Filters) Gradient Magnitude

In the second part, I used a single convolution instead of two by creating a derivative of Gaussian filters. Since convolutions are associative, we are able to get the same results as with two convolutions.



Part 2: Fun with Frequencies!

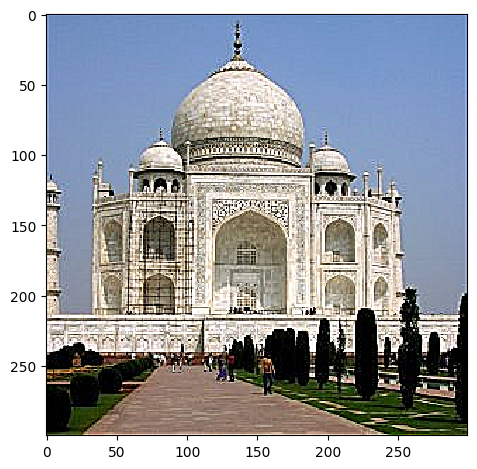
Part 2.1: Image "Sharpening"

For this part, I use the Gaussian filter to get the low frequencies in an image. I then subtract the resulting blurred version (low frequencies) from the original image to get the high frequencies of the image. I then add the high frequencies to the original image to get the "sharper" looking image.

Original
Sharpened
Original
Sharpened
Original
Sharpened
Original
Blur
Sharpen Again

Also for evaluation, pick a sharp image, blur it and then try to sharpen it again. Compare the original and the sharpened image and report your observations.
Despite the image looking sharper than the blurred version before and my best attempts at sharpening it as much as possible, there is a clear loss of information. This can be seen most with edges in the image, such as along the arms, along the edges of the hat, and along the bench, where the contrast in colors is greatest. The sharpened version is unable to replicate the same smoothness in edges because the blurring from earlier removed the high frequency signals. We are unable to get those back exactly and instead have to use the other high frequency signals now in the sharpened version.



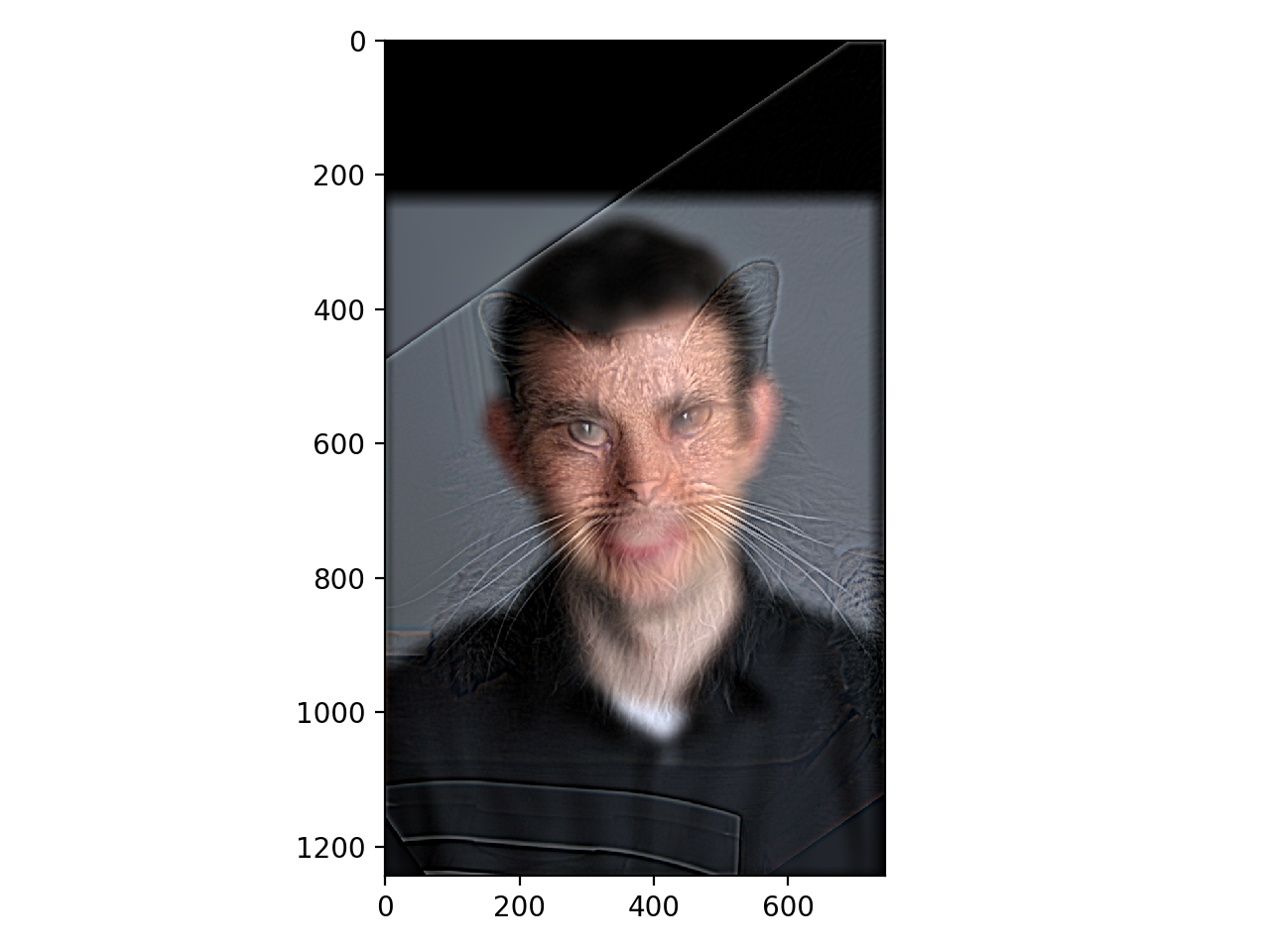
Part 2.2: Hybrid Images

For this part, I separated two images into high frequencies and low frequencies, and combine them together to create hybrid images. The idea behind this is that at far distances, only low frequencies in an image could be seen, while at a closer distance, high frequencies can also be seen. This results in an application of frequencies where you can see two things in one image at different distances.

Derek
Nutmeg
Derek and Nutmeg
Brownie the dog
Dobby
Brownie and Dobby
Smiling
Angry
Failure (Images unusable)
Cat
Dog
Cat and Dog
Log Magnitude Fourier Transform for dog
Log Magnitude Fourier Transform for cat
Log Magnitude Fourier Transform for low filter dog
Log Magnitude Fourier Transform for low filter cat
Log Magnitude Fourier Transform for high filter cat
Log Magnitude Fourier Transform for hybrid image

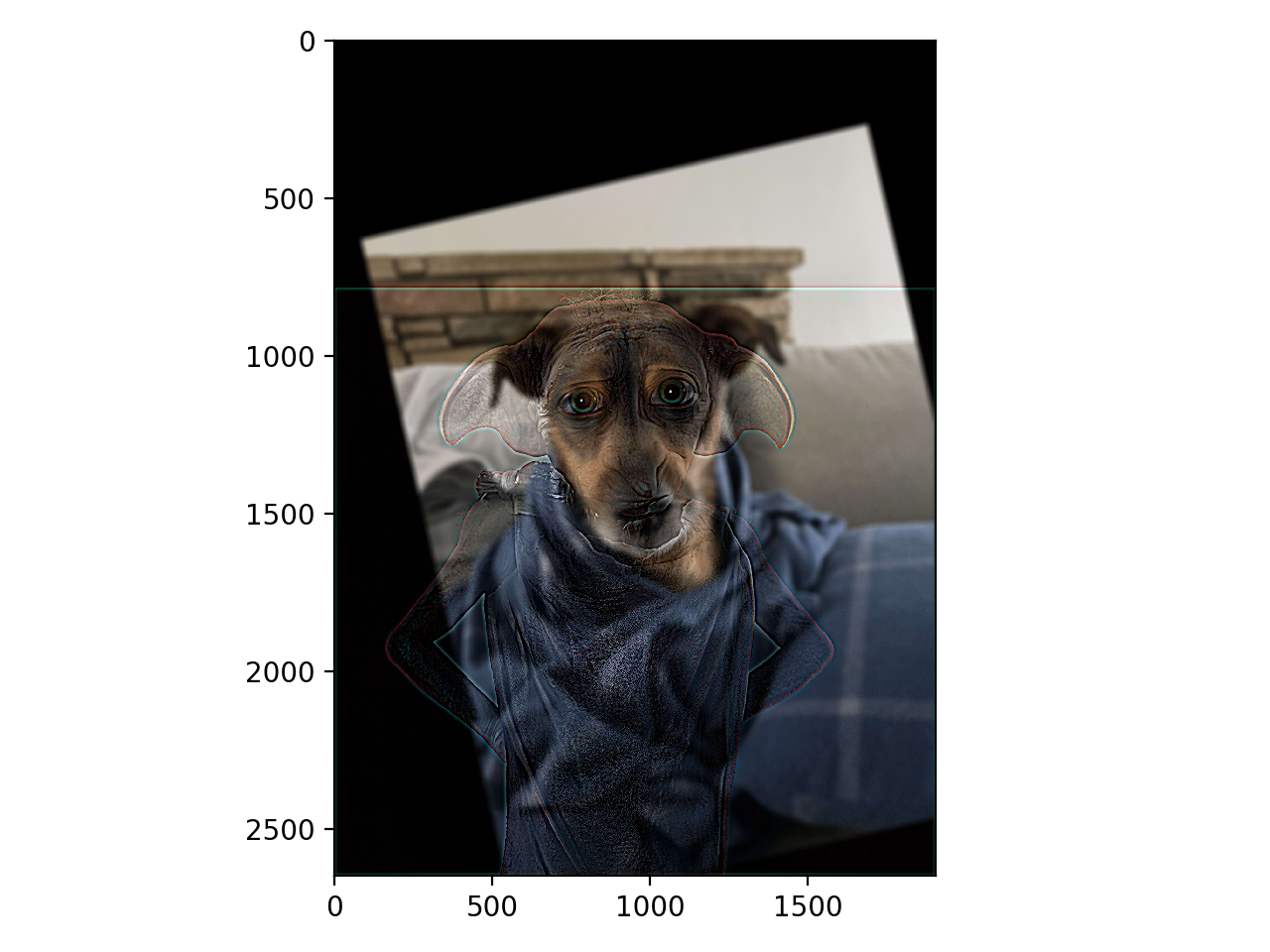
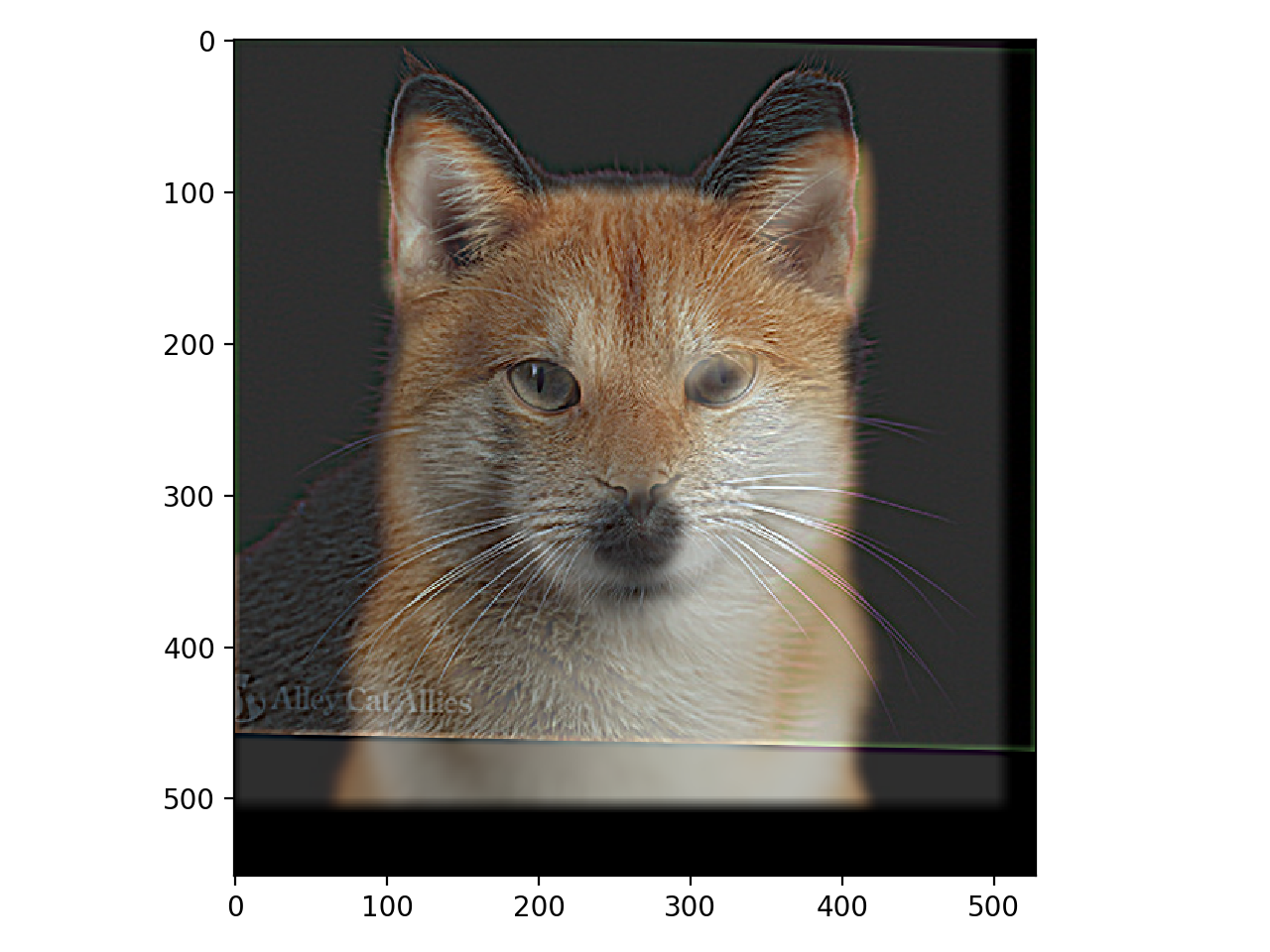
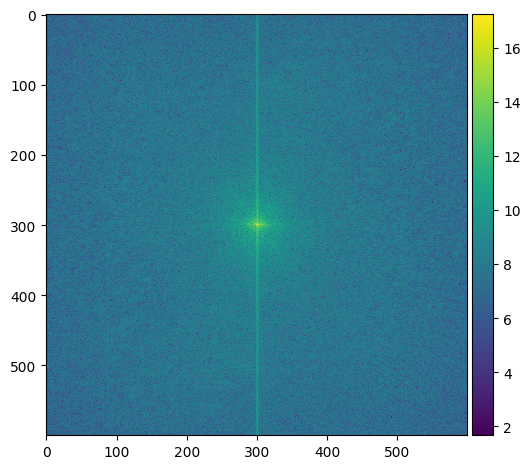
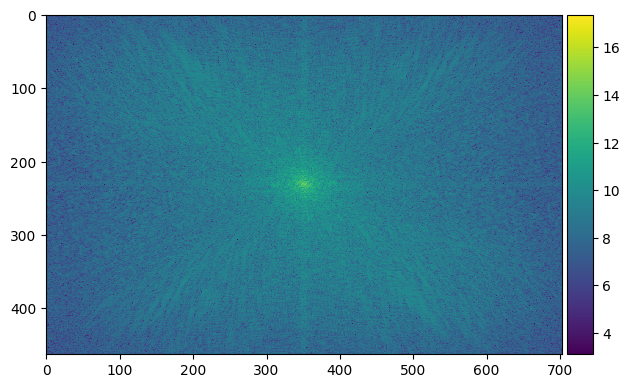
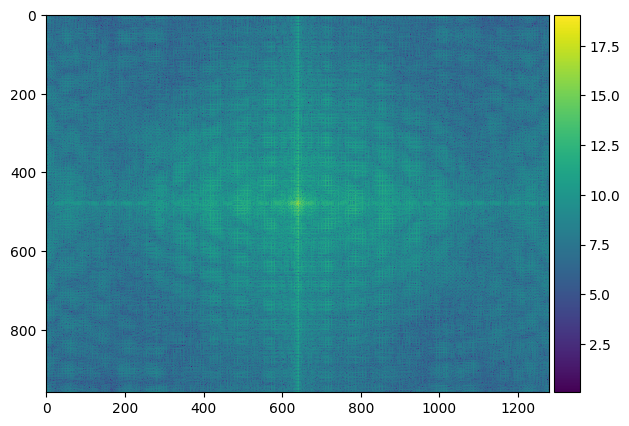
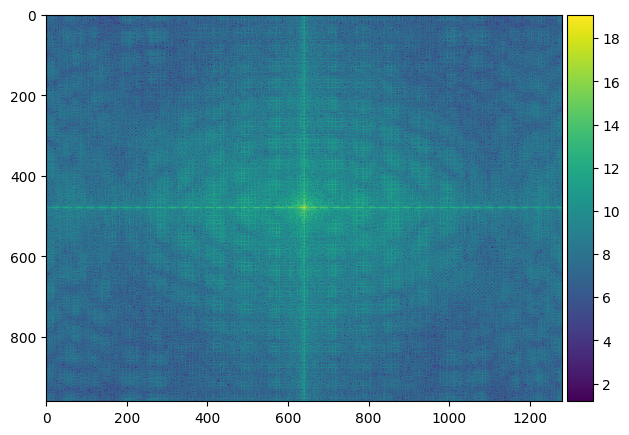
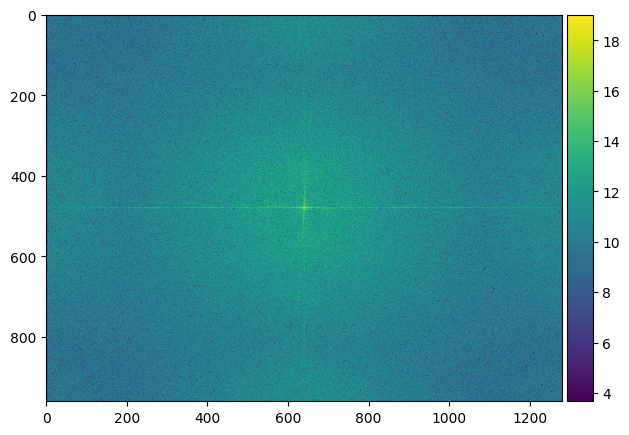
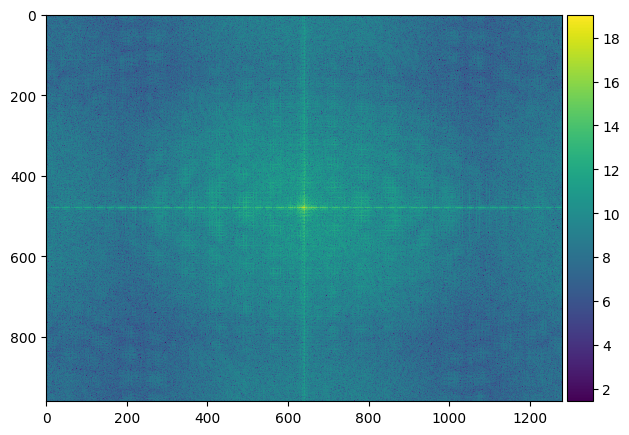
Part 2.3: Gaussian and Laplacian Stacks

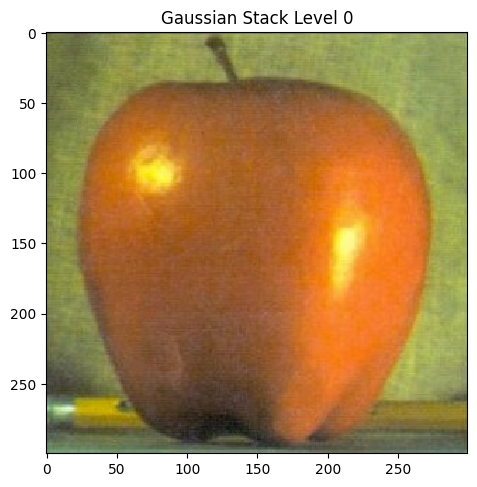
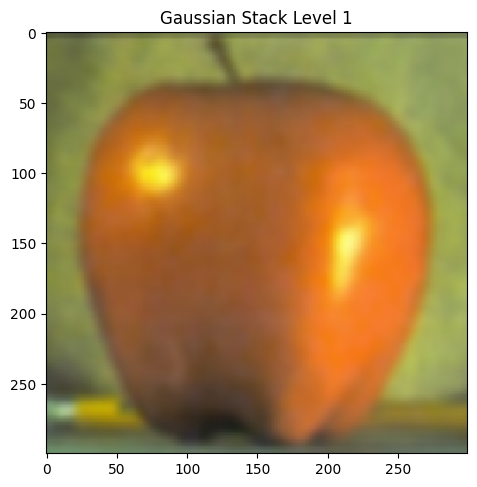
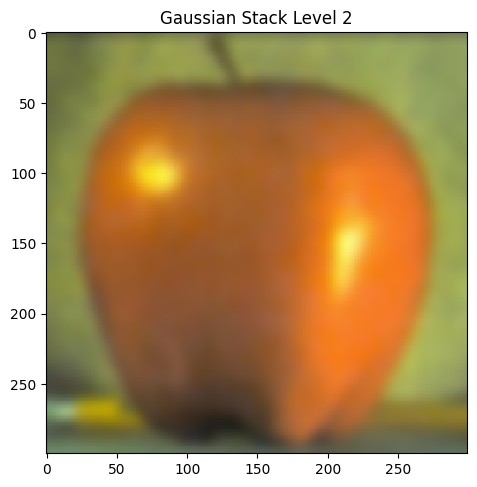
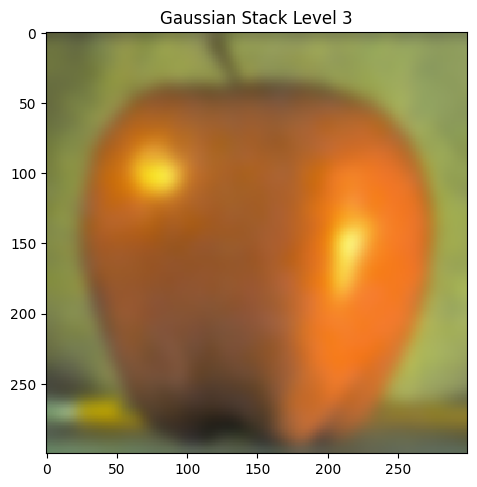
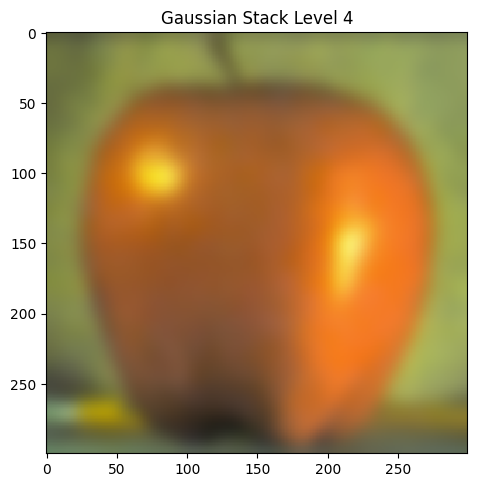
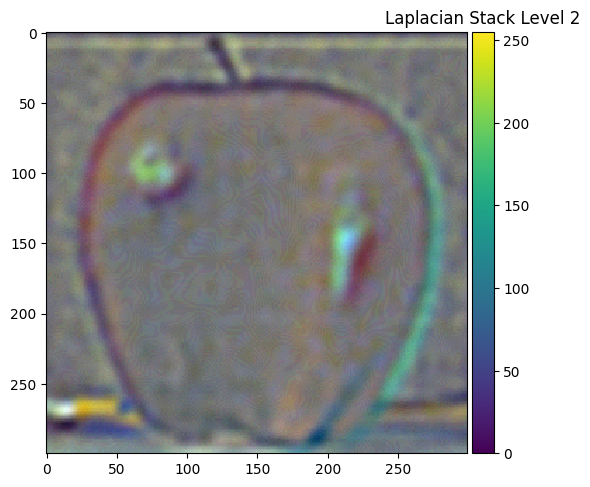
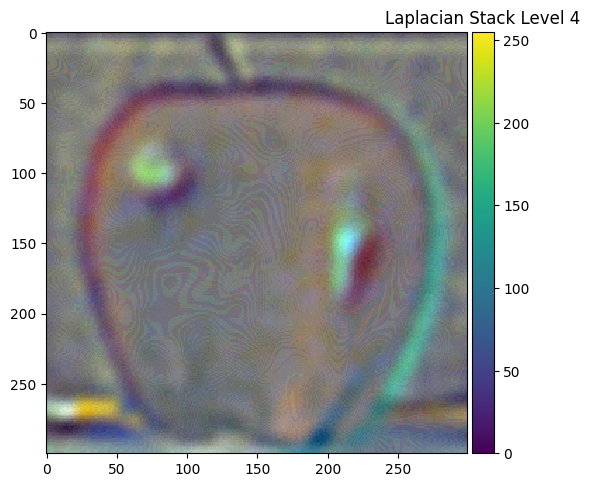
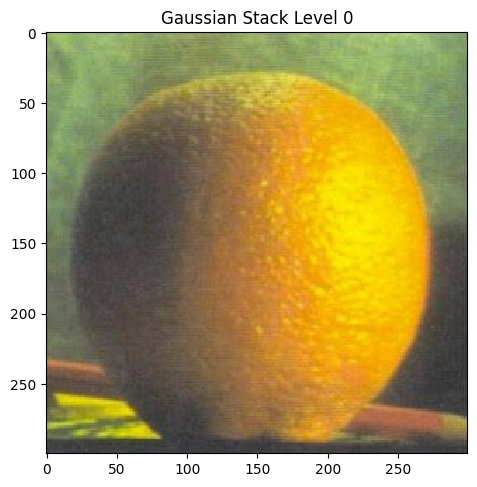
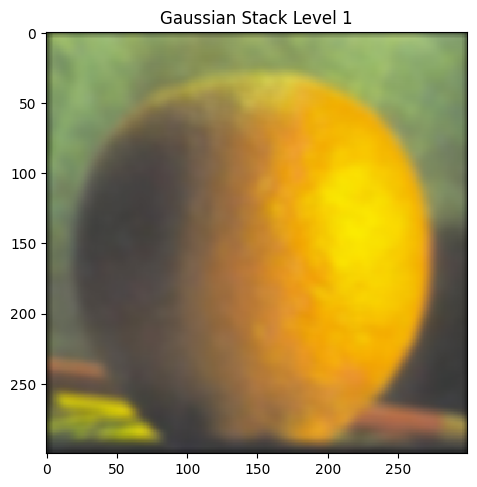
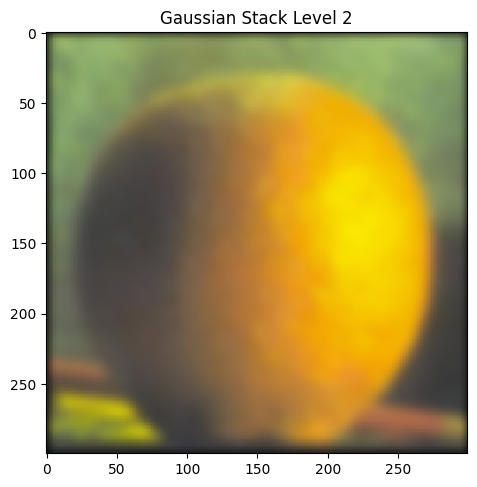
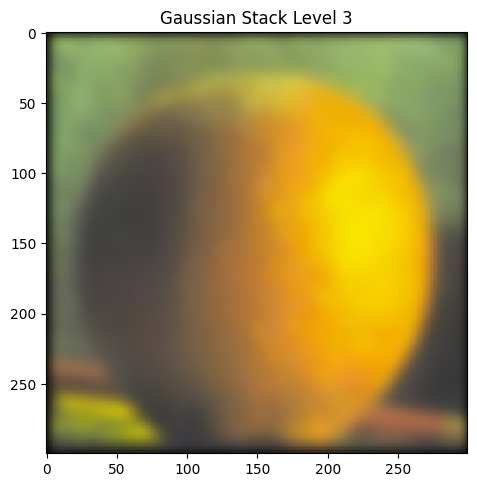
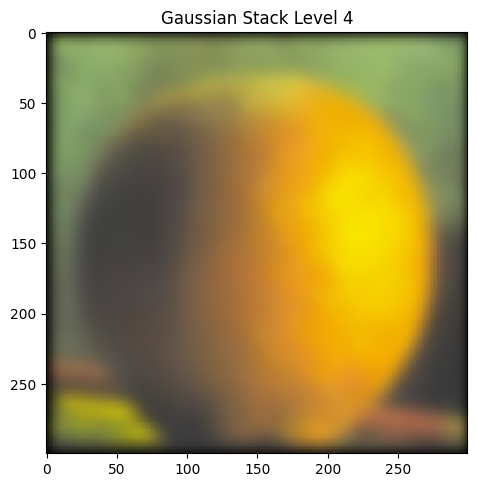
I implemented Gaussian and Laplacian stacks, which allowed for the combining of an orange and apple (the infamous orapple) later.























Part 2.4: Multiresolution Blending (a.k.a. the oraple!)

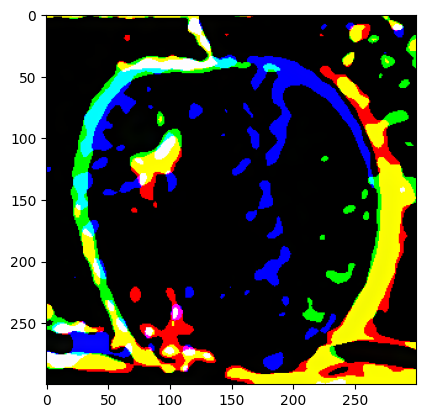
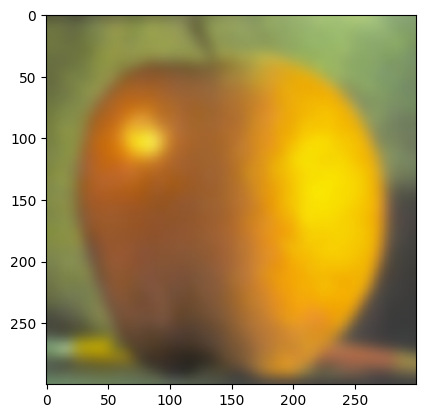
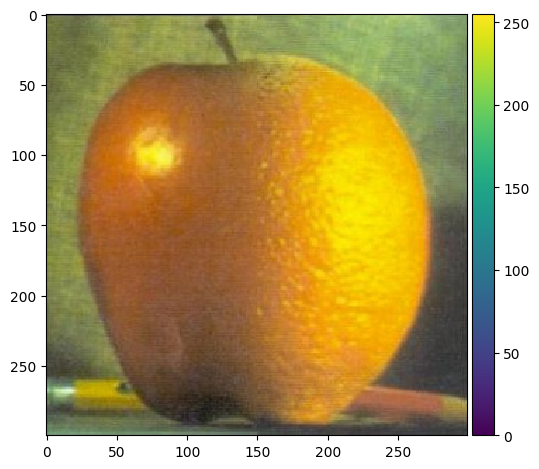
Here I take the Gaussian and Laplacian stacks I implemented previously to blend together the orange and apple. To do this, I first needed a mask which was basically half of each image vertically and created a Gaussian stack for the mask. Then, I blended according to the proposed algorithm in the paper, and summed up the results to get the final orapple image.






Orapple!

Tell us about the most important thing you learned from this project!
The most important thing I learned from this project is that no matter how good code is sometimes, it is equally important to have good images. I ran into so many problems with the hyrbid images and most of them were resolved by simply switching images. Overall, the coolest part about this project is that I found that with just a little bit of math, visually stunning results could be produced!